Harmonic-Frequency Calibration for Accurate Power Measurement
Calibration of e-meters is vital when operating at high frequencies with high harmonics. Failure to do so will result in incorrect measurement and readings. Simple solutions are available to measure harmonics with high accuracy.
When operating at higher frequencies electronic meters are not always able to reliably measure current and voltage. Classic calibration is done at 50 Hz – but higher harmonics are not calibrated and are therefore poorly measured. The resulting margin of error is subsequently greater for higher harmonics.
Measuring harmonics places greater demands on measuring instrumentation (meters in our case). A higher sampling rate requires faster AD converters and more processor calculation power for data processing. These issues are known and well described. But what is never really discussed is the frequency of calibration. It is not surprising, because today’s standards do not affect the status of the network.
What is the behaviour of voltage and current sensor across higher frequencies?
To compute electric power, and consequently the electric energy, it is necessary to precisely measure and digitize both signals – voltage and current. Apart from the magnitude of the signals, the phase shift between them is crucial. Both channels consist of the sensor itself (resistive voltage divider, current transformer) followed by amplifiers, low-pass filters (LPF) and finally the analogue-to-digital converters (ADC’s).
All the components slightly alter the magnitude and phase of the signal – hence the channels should be tested as a complete system, instead of individual elements.
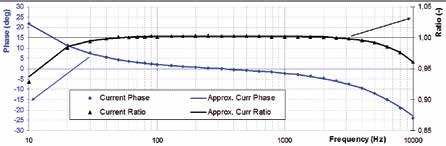
The current channel response consists of high-pass characteristics (current transformer) and low-pass characteristics (following LPF). The response of the voltage channel is represented only by low-pass filter characteristics.
It is evident that there is a significant phase shift of the signal within the frequency range. Hence, calibration must be used in order to correctly calculate the electric power.
Streamlining Calibration Processes
Calibration during the manufacturing process of the energy meter needs to be as fast and easy as possible and it is therefore not appropriate to do it across all points (30 pts.) as in pictures below.
The relationship between the channel errors and frequency can easily be described by the combination of transfer functions of the HPF and LPF. Then only a few points need really to be measured. The solid lines in the picture below represent the results of a three-point calibration process. The nominal frequency (50 Hz) and the decimal multiples – 500 Hz and 5000 Hz (10th and 100th harmonics) were chosen.
The differences between the measured and the computed three-point calibration frequency dependence of the errors are acceptable. Differences are less than 0.2 degrees and 0.2% of phase and ratio errors respectively for current and voltage channels.
Only eight calibration constants are necessary for a description of the dependence of the errors on frequency across both channels – voltage and current. All these constants are stored in the FPGA, which can compute corrections for all discrete frequencies after the FFT process. Applying correction to the results of the FFT calculations ensures the magnitude and phases of the frequency components are correct and the computed electric power is not affected.
Considerations for Channel Behavior and Limitations
Using the correction method assumes the invariable behavior of the channels in real conditions. In this article, a linear DC tolerant current transformer has been used. These CTs have a significant but almost constant phase error (about 4 degrees at 50 Hz). This error is constant even with the presence of DC current.
In contrast, the dual core CTs that are also used in energy meters are able to measure with the DC current presence, but the phase error changes when the DC current occurs. Therefore, this phase error cannot be corrected because there is no information about DC current in the energy meter.
Conclusion
We have shown that it is possible to perform simple frequency calibration of CTs with very little error. All calibration calculations are done in FPGA. This solution provides the ability to accurately measure the energy of high frequency and, as a by-product, develop a frequency analysis of voltage and current in the network.
